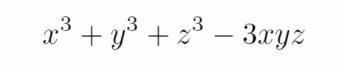【日本語ボランティア】ベトナム(ホーチミン)滞在記
2018年09月02日
ホーチミンの人材派遣センターで日本語を教えてきました!
まず、ホーチミンの街や周辺施設の散策です。
こんな一面も・・・
動物園にも行ってみました!
人材派遣センター TEXGAMEX(株)にて、授業開始です。
私は、日本での就職が決まってもうすぐ日本に行くという学生のクラスに入りました。
授業には、「使える日本語」というコンセプトを中心に会話文を組み立てたり、語彙を選んだものに絵や写真を組み合わせたプリントを用意して行きました。
リピーティングやオーバーラッピングを繰り返しながら定着させ、覚えたものが使えるように工夫をしました。
日本で事前にプリントや教え方の準備をして行ったわけですが、その日の授業が終わると、
「あれも教えたい、これも教えたい。」という思いになり、滞在先のホテルで翌日の授業の準備をしました。
日本で働くために熱心に日本語を学んでいる彼らに、もっと日本人と接する機会が与えられれば良いのにと感じました。
最後の日には、先生方が集まって食事会を開いてくださいました。
こうして滞在記を書いている今頃、写真の彼らは日本で働いていることでしょう。
日本での3年間、5年間が彼らにとって充実した時間であることを願ってやみません。
(ラングアカデミア 代表 中村 景子)
【数学】11の倍数の判定方法
2018年06月09日
自然数が3の倍数であるかの判定法(各位の和が3の倍数)とか9の倍数の判定法はよく知られていますが、あまり11の倍数の判定法は知られていません。
11の倍数の判定法は
『一の位(低位)から左(高位)に向かって奇数番目の和から偶数番目の和を引いたものが11の倍数であれば、11の倍数である。』
例えば、142637 なら奇数番目の和は 7+6+4 =17 、偶数番目の和は3+2+1=6、よって17-6=11 なので11の倍数となります。(142637=11×12967)
9020 なら (0+0)-(9+2)=-11 これも11の倍数です。(計算結果が0や-11,-22 の場合も11の倍数です。)
なぜ成り立つか、6桁の場合について説明します。
というわけです。
似たような仕組みで7の倍数や13の倍数の判定もできます。(1001=7×11×13を利用する)
使う機会ないかな??
※説明部分の②の所にタイプミスがありましたので修正いたしました。
※ご指摘頂いた方、ありがとうございます。
【数学】こんな因数分解は役に立つ?
2018年05月31日
大学受験を目指す高校生や大学生(高専の4年生)以上であれば、
下記の因数分解の問題はどこかで見たとこがあると思います。
もし一般的な解き方を知りたい方は、次の行をコピー&ペーストして検索してください。
x^3+y^3+z^3-3xyz
今回は、行列式を使った因数分解です。
普通科の高校生は行列を習わないので分からなくても仕方ないですが、
高専の4年生以上や大学で行列を習った人ならわかると思います。
※徳山高専は3年の半ばくらいで習います。
①が気付きにくいですよね。
それに、因数分解より行列の方を後に習うか、
または行列自体を習わない人が多いので役には立ちそうにありませんね。
【数学】数式計算サイトの紹介(ただし英語)
2018年05月24日
数学を勉強中であれば、数式をどうやって解くのか分からない場面に遭遇すると思います。
そこで私が時々使っているのが「symbolab」
このサイトの最大の特徴は途中式を表示してくれることです。
(表示してくれないことも多々ありますが。。。)
ただし、このサイトは日本語非対応なので、
英語ができないとダメなのですが・・・
※あと一部有料です。基本的な事は無料でできます。
例えば
line (2,1),(3,5)
と入れると、傾きと切片を計算してくれて、最後に直線の関数を出してくれます。
また、
factor ab-2b+ac-2c
と入れると (a-2)(b+c) と因数分解してくれます。
特に重宝するのは積分で、置換積分の場合は
どの部分を置き換えればよいのかが分かったりします。
他にも、グラフを書いたり、計算結果をpdfファイルに変換してくれたりします。
欠点としては、計算ができるはずの数式を入れても、解答不能とされる場合があります。
数IIIの微分積分や高専で微分積分、線形代数あたりを
習っている人には特に役に立つのではないでしょうか。
入学(進級) おめでとうございます。
2018年04月10日
入学(進級) おめでとうございます。
勉強が以前より大変になるとは思いますが、
新しい環境になったのを機会に、心機一転頑張ってください。
↑ 切戸川の桜です。
【高校入試】山口県の公立高校入学志願者数が出ました。
2018年02月24日
2月24日に平成30年度山口県公立高校入学志願者数が発表されました。
周南地域では、徳山高校が登録者数が340人と例年より多かったのですが、
志願者数は65人減って275人となって、倍率も1.1倍になりました。
登録者数が発表されたときは、志願者数発表時には
徳山高校が減る代わりに、周辺の普通高校の倍率が
少し上がるのではないかと予想していのですが、
殆ど変動がありませんでした。
登録者数より志願者数が明らかに増えたのは、
下松工業(電子機械)と南陽工業(電気)くらいです。
徳山高校の志願者が減った分の人数はどこに行ったのかな?と、
思いましたが、そもそも登録者数に対して志願者数は533人ほど
少ないです。従って、この周南地域だけで、100人程度志願者数が
減るのは当然の事かもしれません。
あと、防府高校の普通科が登録時に304人いて、倍率が1.3倍あったのに、
さらに増えて309人志願しています。普通科の高校で登録時に1.3倍もあったら、
志願時には減るのが通常ですので、志願した人にとっては
予想外だったかもしれません。
兎に角、あとは受験するだけなので頑張ってください。
【高校入試】山口県の公立高校入学志願登録者数が発表されました。
2018年02月16日
2018年2月15日(木)に山口県の推薦入学合格者が発表されたと同時に
公立高校の入学志願登録者数が発表されました。
http://www.pref.yamaguchi.lg.jp/cms/a50300/h30senbatsu/h30touroku.html
※上記をクリックすると山口県のHPが開きます
以前書いた記事(【高校入試】 徳山高校(山口県)の入学定員40人減)から
予想はされていたのですが、周南地域では徳山高校が
入学定員240人に対して100人多い340人が志願していて、倍率は1.4倍となっています。
同地域の下松高校、華陵高校、新南陽高校は例年と変わらない倍率ですが、
光高校と光ケ丘高校が0.8倍と定員を割り込んでいます。
特に光ケ丘高校は例年なら1.4~1.6倍程度であったので、急に減った感じです。
あと、商業/工業系の高校にもいくつか2.0倍を超える高い倍率の学科があります。
因みに、徳山高校は平成27年度(3年前)の入試の時も登録者数の倍率が1.4倍ありました。
そして、入学志願者倍率は1.3倍になりました。
ただ、この3年前の入試では学区が山口県全体ではありませんでした。
今年は学区が山口県全体なので、どのように倍率が動くか予想が難しいです。
受験する高校の倍率が高い人は、大変悩ましい所ですが
よく考えて受験先を選んでください。
【高校生】大学入学共通テストの平成29年度試行調査の結果速報が出てました。
2017年12月07日
12月4日付の新聞に、大学入学共通テストの
平成29年度試行調査の結果速報が載ってました。
新聞には一部の問題と、今回のテストの批評が載っていますが、
全ての問題は下記にありました。
上記リンクの「試験問題等」のところをクリックして進めば、
全ての問題と正解表などが見れます。
数IAをちょっと見てみましたが、
問題文を理解するのに時間が掛かる・・・
あと、問題文を正確に理解して、数学の世界(方程式や関数など)に
変換するという能力が高くないと良い点は出ないでしょう。
別の言い方をすると、実生活とはいかないまでも、より現実的な事象と数学を
結び付ける能力が必要ということです。
まだ、実施まで3年間あるので、色々変わるとは思いますが、
このままだと数学の時間に、生徒に色々な問題文を読ませて
問題文の内容を自分の言葉や図などで答えさせる事をする
必要がありそうです。
もう12月・・寒くなりました。
2017年12月02日
寒くなりました。
早いもので、もう12月です。
駅の方に行ったら、もう毎年恒例のイルミネーションが点灯していました。
11月25日に点灯式があったようです。
参考:周南冬のツリーまつり2017
さらに、徳山駅は工事のための仮囲いが外されています。
電気が点いている所を見ると、内装工事をしているようです。
オープンは平成30年2月3日(土曜日)9時30分の予定だそうです。
参考 : 徳山駅前賑わい交流施設
徳山駅、利用しやすくなってるといいですね。
※冬期講習の案内をもうすぐ出します。 もう少々お待ちください。
【高校入試】 徳山高校(山口県)の入学定員40人減
2017年07月12日
7月10日に
が山口県のホームページに公開されました。
試験実施日は平成30年3月7日(水)で、
合格発表が平成30年3月15日(木)です。
その他、試験科目や試験時間などは例年通りです。
詳しくは、山口県のホームページを見てください。
例年通りか・・・・と思っていたら、
周南地域では、徳山高校普通科の入学定員が40人減の240人になっていました。
2年連続定員割れしていたのが、原因かと思われます。
これで、徳山高校はちょっとハードルが高くなったので、
他の高校に変更する生徒さんも出てくる可能性もありますね。
どの程度影響があるかわかりませんが、
志望校に受かるようにしっかり勉強しておきましょう。
それにしても、県内は軒並み定員を削減してます。
過去の志願者数とかを見ると、そこまで生徒の数は変化していなので、
ずっと供給過剰状態だったのかな??
中国地方、梅雨入りしました。
2017年06月11日
6月7日ごろ中国地方が梅雨入りして、雨がうっとうしい時期になりました。
この時期の花と言えばアジサイ。
昔撮った写真です。ちょっと変わった形のアジサイです。
たぶん、Nikon 80-200 F2.8D のレンズを使って撮ったものだと思います。
あと、この季節はホタルを見に行くことが多いです。
周南市の大道理とかで見れますよ。午後8時くらいが見頃です。
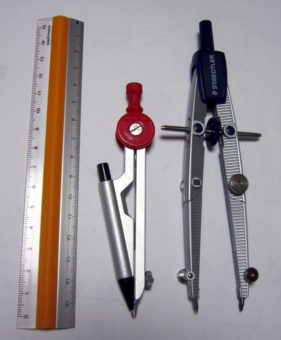
【文房具】中車式の学習用コンパス(ステッドラー スクールコンパス)
2017年05月14日
生徒さんがコンパスを使っているところを見ていると、
たまに使いづらそうにしている子がいます。
長く使っていてボロボロになっていたり、調整が出来ていなかったり・・・
特に、使用中にコンパスの幅が変わってしまう事がよくあります。
原因は下の写真で矢印で示してある支点の部分のネジが緩んでいることが多いです。
そのような場合は、ネジを閉めて調整してください。
中学生が数学で作図をする時は、コンパスを5cmとか3cmとか特定の幅に拡げることは少なく、
それより、使用中にコンパスの幅が変わらない事の方が重要です。
よって、コンパスを広げるのにちょっと固めくらいに調整することをお勧めします。
それでも使っていれば、また緩んできてしまいますし。
力の入れ具合でコンパスの幅が狂ってしまうこともあります。
そこで、中車式の小中学生向けコンパスがあります。
※上の画像やリンクをクリックするとAmazonが別ウインドウで開きます。
真ん中にある中車を回して幅を調節する方式です。
中車のネジでコンパスの足が固定されるので使用中に幅が狂うことはほとんどありません。
注意点としては、このコンパス、大きいです。
生徒さんたちが普通使っているのは上の写真の小さい方のコンパスで、
それに比べて、3cmくらい長いです。たかが3cmですが、結構大きく感じます。
大きいので使いやすいと感じる人と、逆に大きすぎて使いにくいと感じる人もいると思います。
それから、下図のように付属のアダプターを取り付けて、鉛筆などに変えることができます。
ただ、アダプターに取り替える際は、元の足を引き抜くのにちょっと力がいるので
小学生の場合は保護者の方にやってもらった方が良いと思います。
替え芯ですが、ノギスで測ったら直径2mmでした。
ちなみに、付属している替え芯は青いケースに1本だけです。
欠点としては、プラスチック製なのに値段が高いです。
とは言っても、中車式では一番安い方です。
それと、ケース自体はそこそこ頑丈なのですが、中にある底敷きのプラスチックがペコペコです。
購入したコンパスは姪にプレゼントしてしまったので手元にはありませんが、
今度、使用した感想を聞いて、何かありましたら追記したいと思います。
【数学・算数】 中学受験する小学生の算数は難しい
2017年05月10日
この前のゴールデンウイークに東京から小学6年生の姪が遊びに来ました。
姪が通っている塾のテストが近いので勉強道具も持ってきてました。
母親(私の妹)は「算数は分からない!」言うので、私が見ることに。。その一部を紹介。
(問1) 12で割ると7あまり、8で割ると3あまる整数のうち、400に最も近い数をもとめなさい。
(問2) 630 の約数は何個ありますか。
(問3) 101と122をそれぞれある整数で割るとどちらも割り切れず、あまりが等しくなりました。
ある整数として考えられる数をすべて求めなさい。
※問題の数値は変えてあります。また、小学生なので「整数」とは0及び正の整数を指します。
これって。。。高校1年生の問題じゃないの???
(問2)なんてゴールデンウイークに入る前に高校生に教えたばかり。
中学受験する子の算数は難しいですね。
~~~
ちなみに答を高校生向けに行うと、
(問1) 求める整数をNとして、12で割った商をa, 8で割った商をb とすると,
N=12a+7, N=8b+3 より
12a+7=8b+3 整理すると 12a-8b=-4
辺々4で割ると、 3a-2b=-1 ・・・①
a=1, b=2が解の1つであるから、 3・1-2・2=-1 ・・・②
両辺①-②をすると、 3(a-1)-2(b-2)=0
3と2は互いに素なので整数kを使って
a-1=2k, b-2=3k すなわち, a=2k+1 ・・・③, b=3k+2 と表せる。
③をN=12a+7に代入して, N=12(2k+1)+7=24k+19 ・・・④
400に近い数字なので 24k+19=400を解くと k=15.875
kは整数なので近い整数はk=16 これを④に代入して
N=24・16+19=403
よって答は 403 ■
(問2) 630 を素因数分解すると
630=2×3×3 ×5×7
よって、2×3×2×2=24 答 24通り■
※これは、数Aの教科書に載っているので略解にしました。
※小学生も高校生と解き方は同じです。
(問3) ある整数をa, あまりをRとして、101と121のそれぞれの商をn, m とすると
101=an+R ・・・①
122=am+R ・・・②
122 > 101 , a > 0 より, am+R > an+R
したがって、m>n すなわち m-n >0
辺々②-① を行うと 21=a(m-n)
すなわち、a は21の約数{1.3.7,21} が必要条件である。
このうち、aは101と122のどちらも割り切れないことから
101と122のいずれかの約数であるものは十分条件を満たさないので
1は除外される。よって、答は3, 7, 21 ■
因みに 3で割ると 余りは2、 7で割ると余り3、 21で割ると余り17です。
~~~
これでは親も大変だ~。
私なんか小学生の頃は遊んでばかりだったけどな~
【中学生】新学習指導要領で聖徳太子が復活?
2017年05月07日
前回の記事『聖徳太子が「厩戸王」に・・・』で聖徳太子が厩戸王に変わるかもしれないとブログにかきました。
ところが、どうやら戻った?ようです。
そこで、新学習指導要綱(案)と公示された新学習指導要綱の該当記述部を比べてみました。
学習指導要綱(案)では、
”「律令国家の確立に至るまでの過程」については, 厩戸王( 聖徳太子)の政治,大化の改新
から律令国家の確立に至るまでの過程を,小学校での学習内容を活用
して大きく捉えさせるようにすること。”
全文は、http://search.e-gov.go.jp/servlet/PcmFileDownload?seqNo=0000154962 参照してください。
(※リンク切れ注意)
となっていました。 新学習指導要綱では、
“「律令国家の確立に至るまでの過程」については, 聖徳太子の政治,大化の改新から
律令国家の確立に至るまでの過程を,小学校での学習内容を活用して大きく捉えさせ
るようにすること。なお,「聖徳太子の政治」を取り上げる際には,聖徳太子が古事記や
日本書紀においては「厩戸皇子」などと表記され,後に「聖徳太子」と称されるようにな
ったことに触れること。“
全文は、http://www.mext.go.jp/a_menu/shotou/new-cs/__icsFiles/afieldfile/2017/04/26/1384661_5_1.pdf を参照してください。
平成27年の学習指導要綱 と比べると、黒字の部分は変わらず、赤字の部分が追加されています。
「厩戸王」追加で触れるということになったようですね。
平成33年(2021年)4月から実施なので、現在、小学3年生の生徒さんから実施ですね。